Korrelationsanalyse in Stata

In diesem Artikel beschreiben wir, wie sich eine Korrelationsanalyse in Stata umsetzen lässt.

Die Daten

Für die Analysen nutzen wir den systeminternen Datensatz auto.dta. Diesen lesen wir in Stata mit folgenden Befehl ein.

Der Datensatz umfasst diverse Merkmale N = 74 Automodelle, zu denen 12 Merkmale erhoben wurden. Unter Anderem befinden sich im Datensatz Hersteller- und Modellangaben, der Preis, Gewicht und Länge der Fahrzeuge. Kommende Grafik zeigt eine Auflsitung aller Merkmale des Datenmaterials.

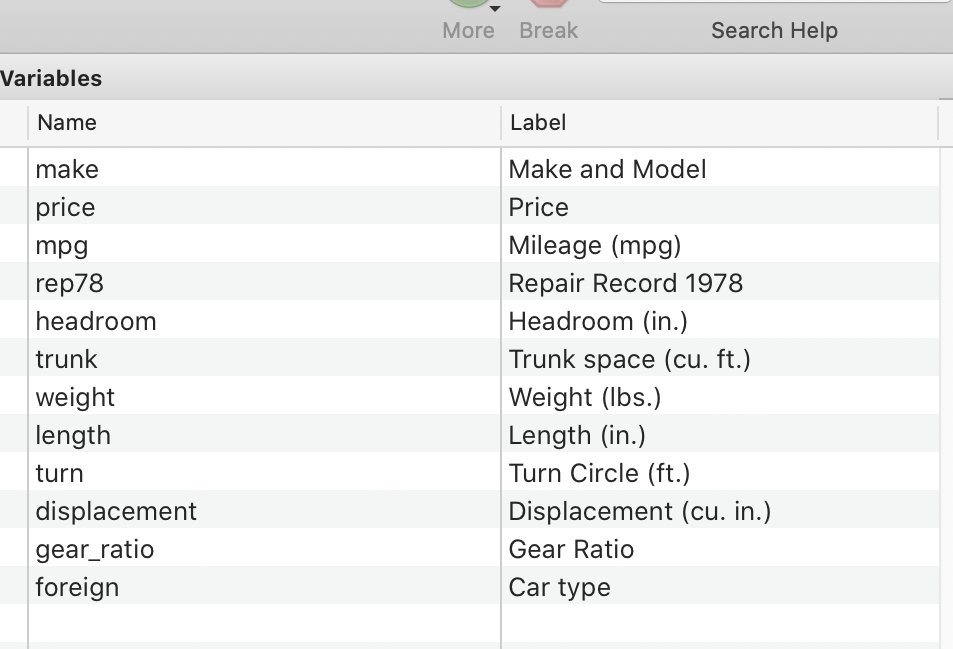
Wir möchten den Zusammenhang zwischen Länge und Gewicht eines Autos untersuchen. Dies werden wir im Folgenden tun.

Die Analyse

Beide Merkmale Gewicht und Länge sind metrischskaliert. Somit kommt für eine Analyse zunächst die Pearson Korrelation in Frage. Wie in dem Bericht Korrelation und "Ausreißer" gesehen, ist eine Korrelationsanalyse mittels des Pearson-Koeffizienten anfällig auf Ausreißer. Somit werden wir zunächst den Zusammenhang visuell in einem Streudiagramm untersuchen.

Mit dem Befehl twoway (scatter length weight) (lfit length weight) erhalten wir die kommende Grafik:

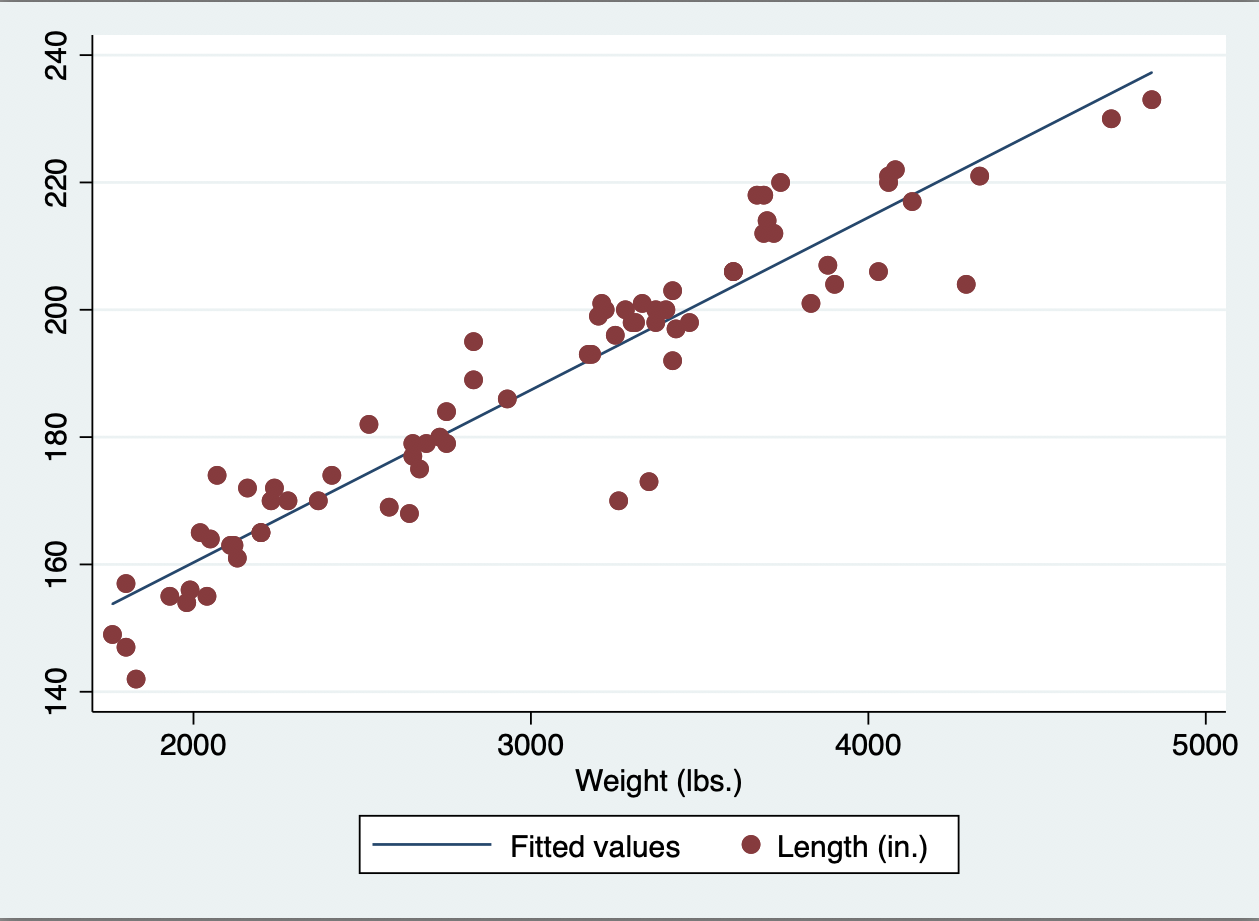
Wir erhalten das Streudiagramm zwischen Länge und Gewicht mit der eingezeichneten Regressionsgeraden. Weiterhin ist zu erkennen, dass mit steigendem Gewicht auch die Länge der Fahrzeuge ansteigt. Ebenso sehen wir, dass sich keine starken Abweichungen von der Regressionsgeraden zeigen. Dies deutet daraufhin, dass keine Ausreißer in den Daten vorliegen. Da keine Ausreißer vorliegen, können wir den Koeffizenten nach Pearson für unsere Korrelationsanalyse verwenden.

Wenden wir in Stata den Befehl pwcorr mit der Option sig an, so erhalten wir die Korrelation, wie auch den Test auf Signifikanz des Korrelationskoeffizientens. Kommende Grafik zeigt das Ergebnis:

Wir sehen die Korrelation zwischen Gewicht und Länge betrug r = 0,95. Sie ist nach Cohen stark positiv. Weiterhin ist die Korrelation signifikant von Null verschieden, p = 0,000. Mit steigender Länge nimmt auch das Gewicht der Fahrzeuge tendenziell zu.